4-Rater Agreement: Unweighted Analysis of Raw Scores

Input Data

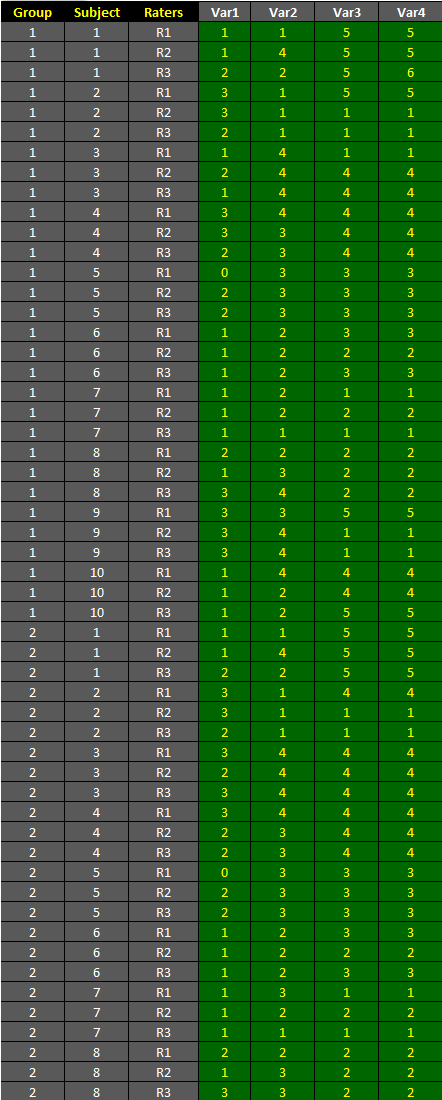
The dataset shown below is included in one of the example worksheets of AgreeStat 360 and can be downloaded from the program. It contains the ratings associated with 4 variables that 3 raters (R1, R2, and R3) assigned to 10 subjects distributed in 2 groups (1 and 2). This data is organized in the long format as shown in the table below.

The objective is to compute unweighted agreement coefficients separately for each of the 4 variables and each group of subjects using AgreeStat360 for Excel/Windows.

Analysis with AgreeStat/360

To see how AgreeStat360 processes this dataset to compute various agreement coefficients, please play the video below.  This video can also be watched on youtube.com for more clarity if needed.

Results

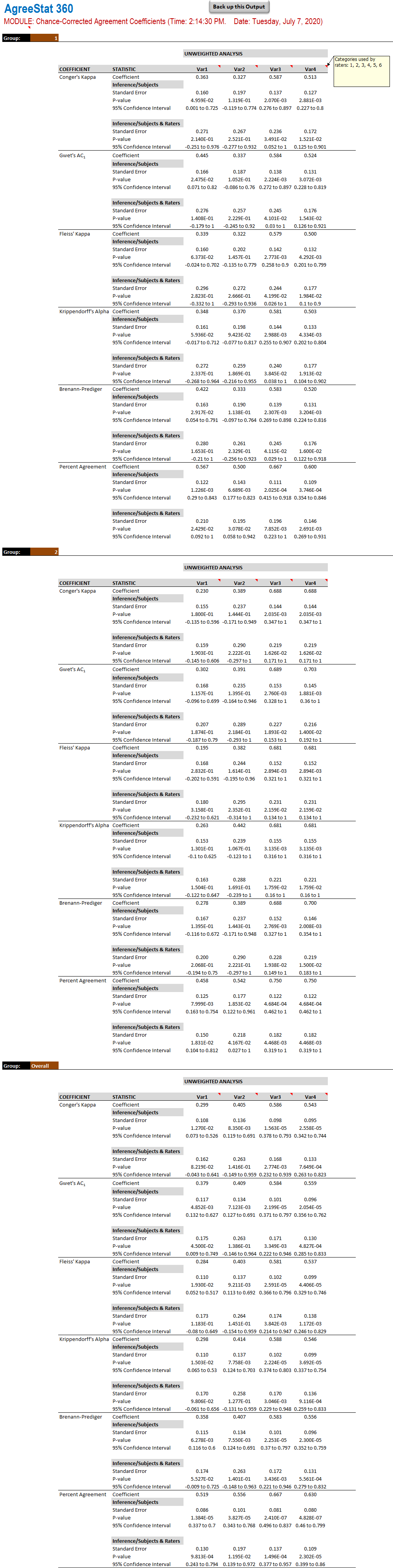
The output that AgreeStat360 produces is shown below.  The analysis is done separately for each of the 2 groups as well as for both groups combined:

• Variables: The 4 rightmost columns of the ouput table contain the various statistics for the 4 variables being analyzed. Each variable name has comments showing the specific scores the raters have used.

• Unweighted analysis: For each group analyzed, 6 agreement coefficients are calculated, including Conger's kappa, Gwet's AC1, and more. Each agreement coefficient is associated with precision measures calculated with respect to the subject sample (i.e. raters are fixed and do not constitue a source of variation), and with respect to both the subject and rater samples considered as 2 independent sources of variation affecting the agreement coefficients. These precision measures are the standard error, the 95% confidence interval and the p-value.