4-Rater Agreement: Weighted Analysis of Raw Scores

Input Data

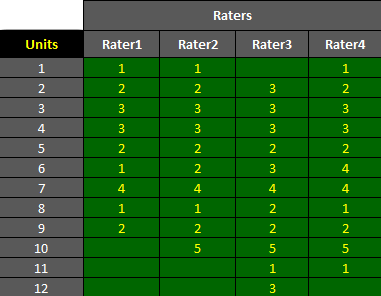
The dataset shown below is included in one of the example worksheets of AgreeStat 360 and can be downloaded from the program. It contains the ratings that 4 raters assigned to 12 units. None of the 4 raters rated all 12 units.  Therefore the dataset contains several missing ratings.

The objective is to compute the weighted extent of agreement among the 4 raters using AgreeStat360 for Excel/Windows.

 

Analysis with AgreeStat/360

To see how AgreeStat360 processes this dataset to produce various agreement coefficients, please play the video below.  This video can also be watched on youtube.com for more clarity if needed.

Results

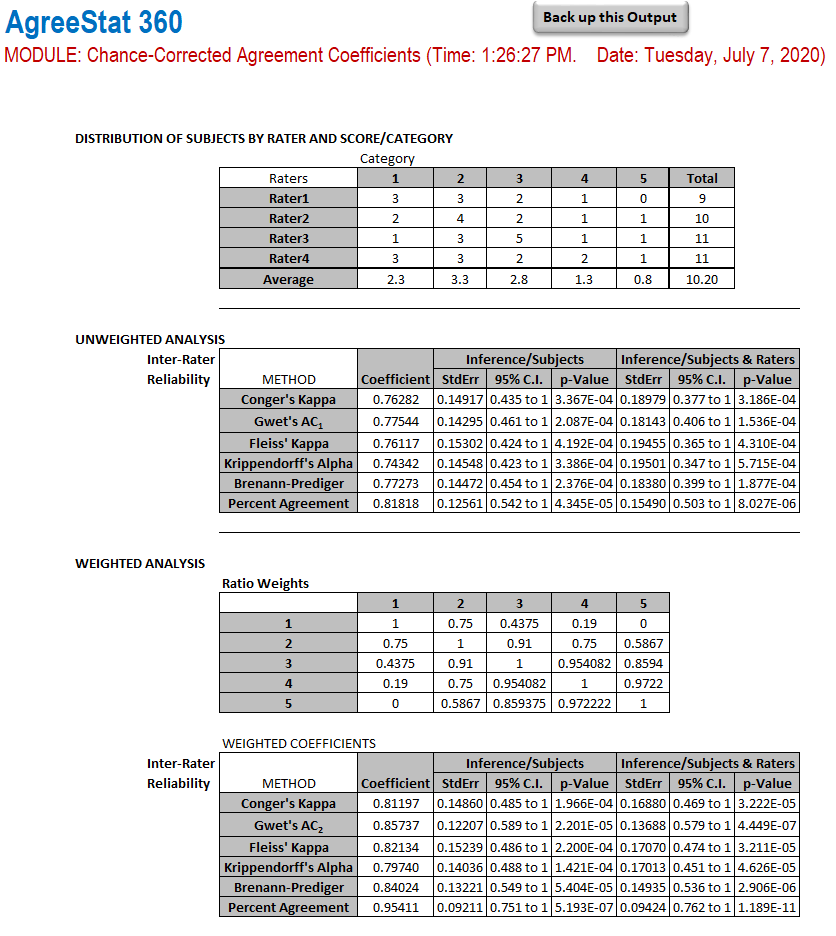
The output that AgreeStat360 produces is shown below and contains 4 parts:

• Summary data: The first part of this output shows the distribution of subjects by rater and category.  The row marginal totals show the number of subjects each rater rated, while the column marginal averages show on average how many subjects each rater classified into each category.

• Unweighted analysis: Six agreement coefficients are calculated, including Conger's kappa, Gwet's AC1, and more. Each agreement coefficient is associated with precision measures calculated with respect to subjects (i.e. raters are fixed and do not constitue a source of variation), and with respect to both subjects and raters. These precision measures are the standard error, the 95% confidence interval and the p-value.

• Weights: The ratio weights used in this weighted analysis are displayed in the third part of this output 

• Weighted analysis: The same 6 agreement coefficients used the unweighted analysis are weighted here. Again, each agreement coefficient is associated with precision measures calculated with respect to subjects and with respect to both subjects and raters considered as 2 sources of variation. These precision measures are the standard error, the 95% confidence interval and the p-value.