Intraclass Correlation
with Multiple Variables
1-Way Random Subject
Effects Model
Input Data
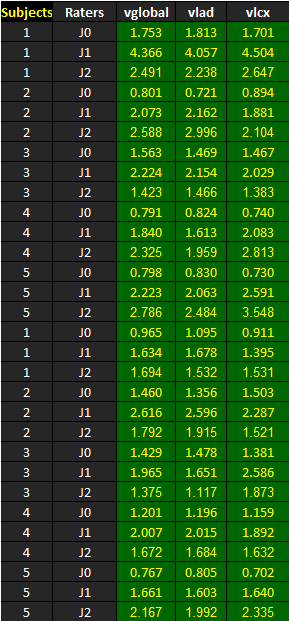
The dataset shown below is included in one of the example worksheets of AgreeStat 360 (This video shows how you may import your own data to AgreeStat360). It contains the ratings that 3 judges J0, J1, and J2 assigned to 5 subjects. Note that the 5 subjects were rated on 3 different variables vglobal, vlad, and vlcx.
The goal is to compute the Intraclass Correlation Coefficients (ICC) under the 1-way random subject effects model. The analysis must be run in batch mode and independently for each variable.
Analysis with AgreeStat/360
To see how AgreeStat360 processes this dataset to produce various agreement coefficients, please play the video below. This video can also be watched on youtube.com for more clarity if needed.
Results
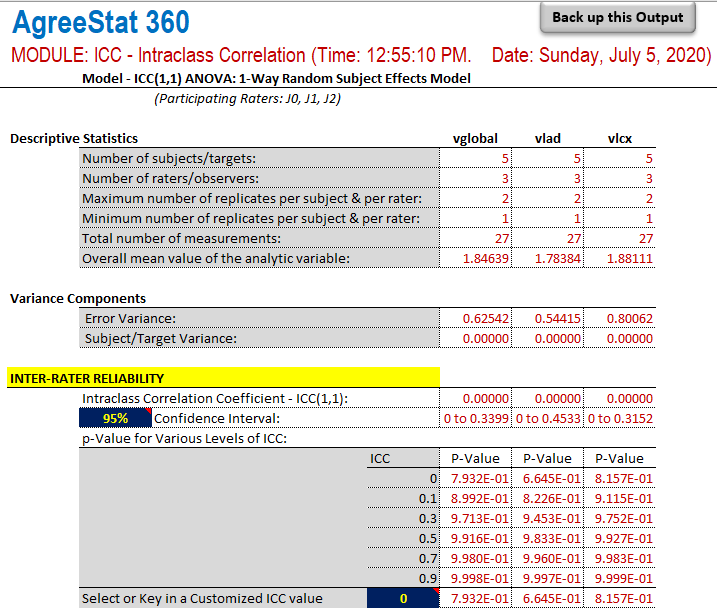
The output that AgreeStat360 produces is shown below and has 3 parts. The basic descriptive statistics constitute the first part. The second part shows the variance components, while the third part shows the inter-rater reliability estimate along with its precision measures. No intra-rater reliability can be calculated under the current model.
Each of the 3 parts of this output contains statistics separately for each of the 3 analytic variables vglobal, vlad, and vlcx.
-
Descriptive statistics: The first part of this output displays basic statistics about the number of non-missing observations for each variable as well as their mean values or number subjects.
-
Variance components: This section will typically show the error and subject variances. These variance components are used for calculating the intra-rater coefficient, and could help explain its magnitude.
-
Inter-rater reliability: This part shows the inter-rater reliability coefficient for each of the 3 analytic variables, their confidence intervals and associated p-values. If needed, you can modify both the confidence level and the ICC null value to update the corresponding confidence intervals and p-values.