Beginner's Guide to Principal Components
by Kilem Li Gwet, PhD

Return to the Book Collection

Principal Component Analysis (PCA) is a statistical technique (not a machine learning algorithm) widely used today for dimensionality reduction of a large dataset.  It is believed to have been invented in 1901 and has been used by statisticians and social scientits for more than 100 years.  However, the interest in PCA has dramatically increased in the era of big data and many modern data processing systems used a version of it.

How exactly does PCA reduce dimensionality? What price do we pay for reducing dimensionality? Look at Figure 1. It shows a scatterplot of original data points in red color. Any exploratory analysis of that data requires that we look at both the $x$ and the $y$ dimensions. Therefore, we are dealing with a 2-dimensional problem where each data point is represented by 2 coordinates $(x,y)$ on the standard coordinate system defined by the 2 basis vectors $(\vec{\imath},\vec{\jmath})$.  

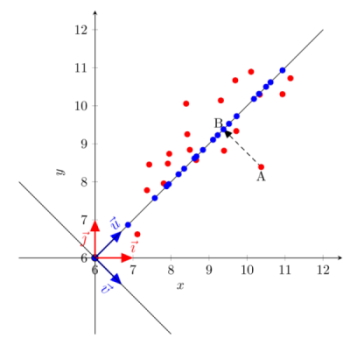
Principal Component Analysis

Figure 1: Orthogonal projection onto the first principal component
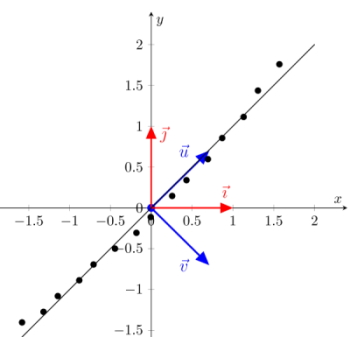
Principal Component Analysis

Figure 2: Almost perfect representation of data points on the first principal component

Here is a fundamental fact all beginners must understand about PCA:

There is no requirement whatsoever to use the standard coordinate system that the 2 basis vectors $(\vec{\imath},\vec{\jmath})$ define. As a matter of fact, any 2 orthogonal vectors can define a new and valid coordinate system.  It turned out that some special orthogonal vectors define coordinate systems that are convenient for analysis.
Consider for example the 2 orthogonal vectors $(\vec{u},\vec{v})$ in Figure 1. Vector $\vec{u}$ defines the dimension along which the data points vary the most, while vector $\vec{v}$ defines the dimension along which the data vary the least.  If you want to analyze your data on a single dimension, it is certainly the dimension defined by vector $\vec{u}$ that you will want to retain. The data points in blue color are the orthogonal projections of the original red data points onto the axis defined by vector $\vec{u}$, and represent the numbers you will analyzed in the reduced one-dimensional space. Vector $\vec{u}$ is called the first (and most dominant) principal component, while vector $\vec{v}$ is the second and least dominant principal components.

The study of Principal Components amounts to doing the following:

All three tasks defined above and more are discussed in details in my book entitled Beginner's Guide to Principal Components. You may download the first few pages of each chapters for information below. Errors  and typos contained in this book as reported by various readers and myself can be found in the errata page. Please check there regularly for new reports.

Contents

Beginner's Guide to Principal Components by Kilem L. Gwet, PhD

beginner's guide to principal components

You can see from Figure 1 that when you reduce your space from 2 dimensions to only one, your analysis is considerably simplified.  However, you also expect to lose some information contained in your data.  That lost is often more or less negligible. In Figure 2 however, the lost of information resulting from dimensionality reduction will surely be negligible.  This is due to most data points lining up very closely along the direction defined by the most dominant principal component $\vec{u}$.